Date: February 22, 2022

Relevant Textbook Sections: 4.4

Cube: Supervised, Discrete or Continuous, Nonprobabilistic

Lecture Video

Announcements

1. HW2 is due this Friday
2. Midterm 1 is this Tuesday
3. March 3, Thursday after midterm we have our Ethics module

Lecture 9 Summary

• Optimizing the Neural Network
• Detour: Vector Chain Rule
• Let's Now Finish The Optimization
• Let's Generalize Everything
• Why does this all work?

Optimizing the Neural Network

Last time, we talked about neural network architectures. Today, we'll discuss how neural networks can be optimized. (Spoiler: it's a lot of chain rule.) We'll use $\sigma$ as our activation function in lecture, but you can replace it with other activation functions like tanh or ReLU as well.

To optimize a neural network, we'd like to choose parameters $W$ that minimize the network's loss. We can find these parameters via gradient descent, but first we'll have to calculate the gradients of the network's loss with respect to the parameters.

So, we are trying to find: $$\frac{\partial L}{\partial W}$$ For some input $x_n$, the loss function $L$ is some way to measure the difference between the true value $y_n$ and the value $f_n$ our model predicts for $x_n$. Previously when discussing regression, we used $\hat{y}_n$ to represent the model prediction instead of $f_n$. Since the loss function must depend on $f_n$ (which in turn depends on the model parameters we're trying to optimize), we'll need to use chain rule: $$\frac{\partial L}{\partial W} = \frac{\partial L}{\partial f_n} \frac{\partial f_n}{\partial W}$$

Loss Function For Regression

We've been using the least squares loss for regression. $$L(w) = \frac12 \cdot \sum_n(y_n - f_n)^2$$ The derivative with respect to $f_n$ will be: $$\frac{\partial L}{\partial f_n} = \sum_n (y_n - f_n)(-1)$$ Note: If we swapped $L$ to be another loss function, the only effect on the whole original expression $\frac{\partial L}{\partial W}$ is a change in $\frac{\partial L}{\partial f_n}$. The rest of the gradient, $\frac{\partial f_n}{\partial W}$, remains the same.

Loss Function For Classification

For classification, a good loss function choice might be logistic loss. For a binary classification case, we define the following:

$$p(y=1|x) = \sigma(f_n) = \frac{1}{1 + \exp(-f_n)}$$ $$p(y=0|x) = 1 - \sigma(f_n) = \frac{1}{1 + \exp(f_n)}$$ Now, we can define the logistic loss function using the terms above:

\begin{align*} L(w) &= \sum_n y_n \log p(y=1|x) + (1 - y_n) \log p(y=0|x) \\ &= \sum_n y_n \log \sigma(f_n) + (1 - y_n) \log (1 - \sigma(f_n)) \end{align*} Also remember the following helpful tip for the derivative:

$$\frac{\partial\sigma(z)}{z} = \sigma(z)(1 - \sigma(z))$$ So then the derivative is:

$$\frac{\partial L_n}{\partial f_n} = y_n \frac{1}{\sigma(f_n)} \sigma(f_n) (1 - \sigma(f_n)) + (1 - y_n) \frac{1}{1 - \sigma(f_n)} \sigma(f_n)(1 - \sigma(f_n))(-1)$$ We can simplify:

$$\frac{\partial L_n}{\partial f_n} = y_n (1 - \sigma(f_n)) - (1 - y_n) \sigma(f_n)$$ This would be something we can calculate if we knew what $f_n$ was. So to get the gradient, we'll first have to use the current weights $W$ to calculate $f_n$ (a "forward pass"), then use $f_n$ to find the gradient (a "backward pass") and make our update step along the gradient.

Preview for intuition: in the forward pass, we start with an input $x_n$ and move forward through the layers of the model to figure out what the output $f_n$ would be (along with what other activation values in the network are). In the backward pass, the values we've calculated flow backwards to be used in chain rule products. (When we're working with many layers, $f_n$ will rely on $w_0$ a parameter in the first layer with $w_0$ nested inside many other products and activation functions. So then $\frac{\partial f_n}{\partial w_0}$ will involve a lot of chain rules.) These chain rule products become the gradients we are looking for.

Detour: Vector Chain Rule

We will take a slight detour now in order to gain the tools we need to do the back propagation. Say we had nested functions as follows: $$y = f(u) = f(g(h(x)))$$ $$u = g(v) = g(h(x))$$ $$v = h(x)$$

All Scalars

If we had all scalars, and we wanted to look for $\frac{\partial y}{\partial x}$, then we can simply apply chain rule:

$$\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u}\frac{\partial u}{\partial v} \frac{\partial v}{\partial x}$$

If x (size $D$) was a vector

$$\nabla_\mathbf{x}y = \frac{\partial y}{\partial u} \frac{\partial u}{\partial v} \nabla_\mathbf{x}v$$ Where $\frac{\partial y}{\partial u}$ and $\frac{\partial u}{\partial v}$ are scalars, and $\nabla_\mathbf{x} v$ is a $1 \times D$ vector describing how each dimension of $\mathbf{x}$ affects scalar $v$.

Note: We are using the numerator layout notation (sometimes known as the Jacobian formulation), where if $\mathbf{y}$ and $\mathbf{x}$ are size $M$ and $N$ vectors respectively, then $\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$ is an $M\times N$ matrix such that $$\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \begin{pmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_N} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_N} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_M}{\partial x_1} & \frac{\partial y_M}{\partial x_2} & \cdots & \frac{\partial y_M}{\partial x_N} \end{pmatrix}$$ $\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$ is known as the Jacobian matrix and represented as $\mathbb{J}_\mathbf{x}[\mathbf{y}]$. Its elements tell us how each element of $\mathbf{y}$ depends on each element of $\mathbf{x}$.

If x (size $D$) and v (size $J$) were both vectors

$$\nabla_\mathbf{x} y = \frac{\partial f}{\partial u} \nabla_\mathbf{v}u \mathbb{J}_\mathbf{x}[\mathbf{v}]$$ $\frac{\partial y}{\partial u}$ is a scalar, $\nabla_\mathbf{v}u$ is a $1 \times J$ vector, and $\mathbb{J}_\mathbf{x}[\mathbf{v}]$ is a $J \times D$ matrix.
$\mathbb{J}_\mathbf{x}[\mathbf{v}]$ measures how each dimension of $\mathbf{x}$ affects each dimension of $\mathbf{v}$ and $\nabla_\mathbf{v}u$ how each dimension of $\mathbf{v}$ affects each dimension of $u$.
Chaining them, $\nabla_\mathbf{v}u \mathbb{J}_\mathbf{x}[\mathbf{v}]$ ($1 \times D$ vector) measures how each dimension of $\mathbf{x}$ affects each dimension of $u$.
Consequentially, $\frac{\partial f}{\partial u} \nabla_\mathbf{v}u \mathbb{J}_\mathbf{x}[\mathbf{v}]$ is a vector of how each $\mathbf{x}$ dimension changes scalar $y$, through all dimensions of $\mathbf{v}$ and $u$.

If x (size $D$) and v (size $J$) and u (size $J^\prime$) were all vectors

$$\nabla_\mathbf{x} y = \nabla_\mathbf{u} y \mathbb{J}_\mathbf{v}[\mathbf{u}] \mathbb{J}_\mathbf{x}[\mathbf{v}]$$ $\nabla_\mathbf{u} y$ is a $1 \times J^\prime$ vector, $\mathbb{J}_\mathbf{v}[\mathbf{u}]$ is a $J^\prime \times J$ matrix, $\mathbb{J}_\mathbf{x}[\mathbf{v}]$ is a $J\times D$ matrix. We still get a vector of how each $\mathbf{x}$ dimension changes scalar $y$, through all dimensions of $\mathbf{v}$ and $\mathbf{u}$.

Let's Now Finish The Optimization

As a refresher, we've had from before: $$\frac{\partial L_n}{\partial \mathbf{w}} = \frac{\partial L_n}{\partial f_n} \frac{\partial f_n}{\partial \mathbf{w}}$$ We already calculated $\frac{\partial L_n}{\partial f_n}$ before, so we need to now calculate $\frac{\partial f_n}{\partial \mathbf{w}}$. Let's say our $f_n = \mathbf{w}^T\mathbf{\phi_n} + b$. If so, that means we have: $$\frac{\partial f_n}{\partial \mathbf{w}} = \mathbf{\phi_n}$$

Example: Let's Complete the Full Expression for the Regression Case

From before for the regression case, we have $\frac{\partial L_n}{\partial f_n} = (y_n - f_n)(-1)$, and now we have $\frac{\partial f_n}{\partial \mathbf{w}} = \mathbf{\phi_n}$, so combined we have:

$$\frac{\partial L_n}{\partial \mathbf{w}} = (y_n - f_n)(-1) \mathbf{\phi_n}$$

Notice that we still need the value $f_n$ to compute the gradient.
How will we get this term? We can first compute $\mathbf{x} \rightarrow \mathbf{\phi_n} \rightarrow \mathbf{f_n}$ and then use that value of $\mathbf{f_n}$ in the gradient.

Recall that $\mathbf{\phi_n} = \sigma (\mathbf{W}^1\mathbf{x} + \mathbf{b}^1)$. How can we get $\nabla_\mathbf{W}\mathcal{L}_n$?

$$\nabla_\mathbf{W}\mathcal{L}_n = \frac{\partial L_n}{\partial f_n} \nabla_\mathbf{\phi_n}f_n \mathbb{J}_\mathbf{W^1}[\mathbf{\phi_n}]$$

Let's Generalize Everything

The process of computing gradients for optimizing neural networks, which was previewed earlier on, is then as follows:

1. Compute $\mathcal{L}(\mathbf{\phi}^{L}(\mathbf{\phi}^{L-1}(\cdots \mathbf{\phi}^{1}(\mathbf{x}))))$ by passing $\mathbf{x}$ through the network $\mathbf{x} \rightarrow \mathbf{\phi}^{1} \rightarrow \cdots \rightarrow \mathbf{\phi}^{L-1} \rightarrow \mathbf{\phi}^{L} \rightarrow \mathcal{L}$ (forward pass) and store all $\mathbf{\phi}^\ell$.
2. Perform the chain-rule backwards:
   • $$\frac{\partial \mathcal{L}}{\partial \mathbf{\phi}^\ell} = \nabla_{\mathbf{\phi}^L}\mathcal{L} \mathbb{J}_{\mathbf{\phi}^{L-1}}[\mathbf{\phi}^{L}] \cdots \mathbb{J}_{\mathbf{\phi}^{\ell}}[\mathbf{\phi}^{\ell + 1}]$$
   • Compute the parameter gradients $$\begin{align*} \frac{\partial \mathcal{L}}{\partial \mathbf{W}^\ell} &= \nabla_{\mathbf{\phi}^L}\mathcal{L} \mathbb{J}_{\mathbf{\phi}^{L-1}}[\mathbf{\phi}^{L}] \cdots \mathbb{J}_{\mathbf{\phi}^{\ell}}[\mathbf{\phi}^{\ell + 1}] \mathbb{J}_{\mathbf{W}^{\ell}}[\mathbf{\phi}^{\ell}] \\ &= \frac{\partial \mathcal{L}}{\partial \mathbf{\phi}^\ell} \frac{\partial \mathbf{\phi}^\ell}{\partial \mathbf{W}^\ell} \end{align*}$$

The following picture illustrates the steps:



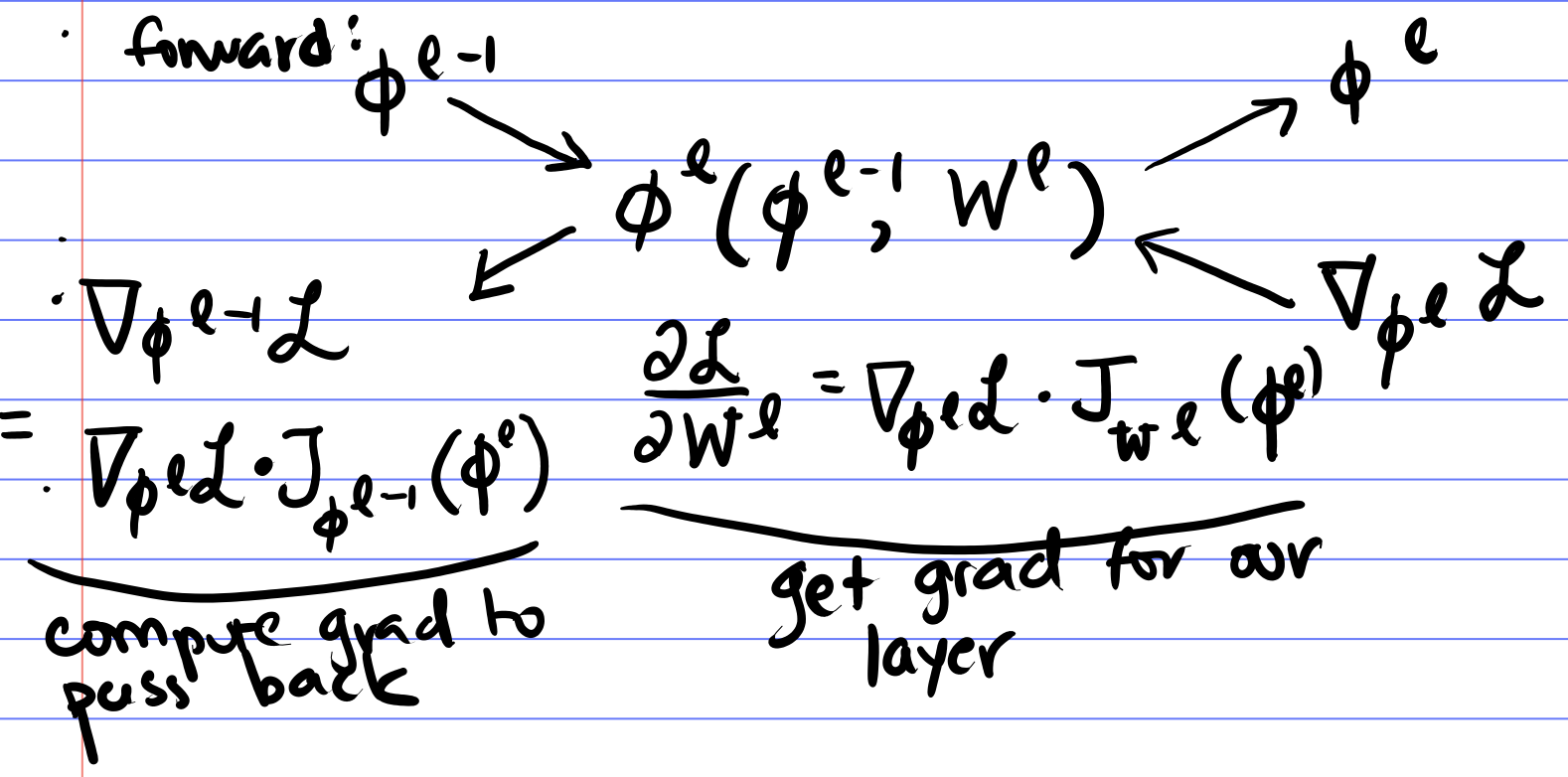
Note: This is called "reverse-mode" autodiff or backpropagation. This is good when the output ($y$) is small and there are many parameters (all the $W$s). It allows for efficient reuse of computed values.

We can also do "forward-mode" diff. Suppose we wanted just a derivative/sensitivity test on $\frac{\partial \mathcal{L}_n}{\partial x_{nd}}$. Then we don't need all the $\frac{\partial \mathbb{\phi}}{\partial W_{jd^\prime}}$ for all $d^\prime \neq d$.
Forward mode goes from the variable $x_{nd}$ to $\mathcal{L}_n$ rather than from $\mathcal{L}_n$ to $x_{nd}$.
We compute $\frac{\partial \mathbf{\phi}^1}{\partial x_{nd}}$, then $\frac{\partial \mathbf{\phi}^2}{\partial \mathbf{\phi}^1}$ all the way up.

Why does this all work?

1. GPUs allow us to do fast, parallelized matrix multiplications.
2. We now have lots of data, and lots of data avoids overfitting. Neural networks are good at interpolating large datasets.
3. Practicalities
   • Theory is lagging, but belief is that the over-parameterization enables easier gradient descent (gradient descent doesn't work in simpler models).